GridSearch for hyper parameter tuning

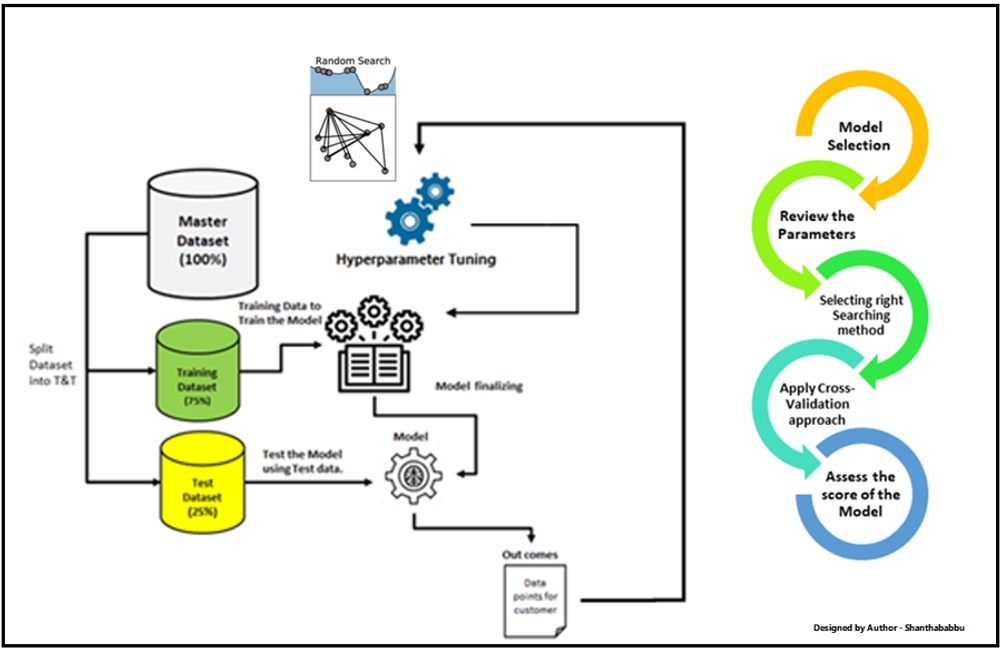
Hyperparameter tuning

All most all the machine learning models have various knobs, dials and parameters that we can set to modify its performance. For example:

• Neural Networks have learning rate and regularization strength
• Convolutional Neural Networks have several layers, number of filters per convolutional layer, number of nodes in the fully connected layers, etc.
• Decision trees have the node split criteria (Gini index, information gain, etc.)
• Random Forests have the total number of trees in the forest, along with feature space sampling percentages
• Support Vector Machines (SVMs) have the type of kernel (linear, polynomial, radial basis function (RBF), etc.) along with any parameters you need to tune for the particular kernel

These knobs, dials and parameters are known as hyper parameters. The processing of modifying this hyper parameters to get improve the performance of our model is called hyper parameter tuning.

Local variables can be added into the HTML using the curly braces syntax:

1. Local variables can be used in curly braces to pass attribute values to both HTML elements and components:
2. Meat sack optimisation - Trying values randomly to see what works. What we students always do!!
3. Analytic solutions - Solve directly through maths
4. Brute force - Try every option (ok if the domain is small and discrete)
5. Grid search - Nested loop, this explodes in higher dimensions.
6. Random search - Try many random params, we use a distribution for each to bias search. This works in higher dimensions.
7. Hill climbing - Similar to gradient ascent but without gradient.
8. Shot gun - Hybrid of random search and hill starts

In this article we will focus on grid search and random search on SVM. SVMs are notorious for requiring significant hyperparameter tuning, especially if you are using a non-linear kernel. Not only do you need to select the correct type of kernel for your data, but then you also need to tune any knobs and dials associated with the kernel — one wrong choice, and your accuracy can plummet. Here is the basic idea on doing hyper parameter tuning:

1. Define a set of hyperparameters you want to tune.
2. Give these hyperparameters to the grid search or random search.
3. These algorithms then automatically examine the hyperparameter search space and attempt to find the optimal values that maximize accuracy.

Grid search and random search are inherently different techniques for hyper parameter tuning like shown in below figure: Before we zoom in to the search further let’s import all the functions and load all the data like below.

Machines learning

Import the necessary packages

from pyimagesearch import config
from sklearn.model_selection import RepeatedKFold
from sklearn.model_selection import GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split
import pandas as pd

Then we will load the dataset, separate the features and labels, and perform a training and testing split using 85% of the data for training and 15% for evaluation.

print("[INFO] loading data...")
dataset = pd.read_csv(config.CSV_PATH, names=config.COLS)
dataX = dataset[dataset.columns[:-1]]
dataY = dataset[dataset.columns[-1]]
(trainX, testX, trainY, testY) = train_test_split(dataX,
	dataY, random_state=3, test_size=0.15)

Finally standardize the feature values by computing the mean, subtracting the mean from the data points, and then dividing by the standard deviation

scaler = StandardScaler()
trainX = scaler.fit_transform(trainX)
testX = scaler.transform(testX)

Grid search

In grid search:

1. We start by defining a set of all hyperparameters and the associated values we want to explore
2. The grid search then examines all combinations of these hyperparameters
3. For each possible combination of hyperparameters, we train a model on them
4. The hyperparameters associated with the highest accuracy are then returned

A grid search is guaranteed to examine all possible combinations of hyperparameters. The problem is that the more hyperparameters you have, the more the number of combinations grows exponentially! And since there are so many combinations to examine, a grid search tends to run very slowly. Lets now initialise our model and define the search pace of hyper parameters to perform the grid-search over:

model = SVR()
kernel = ["linear", "rbf", "sigmoid", "poly"]
tolerance = [1e-3, 1e-4, 1e-5, 1e-6]
C = [1, 1.5, 2, 2.5, 3]
grid = dict(kernel=kernel, tol=tolerance, C=C)

Here we initialize our Support Vector Machine regression (SVR) model. An SVR has several hyperparameters to tune, including:

1. kernel: The type of kernel used when projecting the data into a higher-dimensional space where it ideally becomes linearly separable
2. tolerance: The tolerance for stopping criterion
3. C: The “strictness” of the SVR (i.e., to what degree the SVR is allowed to make mistakes when fitting the data)

In above code we define values for each of these hyperparameters and create a dictionary of the hyperparameters. Our goal will be to search these hyperparameters and find the optimal values for kernel, tolerance, and C.

Lets perform the grid search now: '''python print(“[INFO] grid searching over the hyperparameters…”) cvFold = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1) gridSearch = GridSearchCV(estimator=model, param_grid=grid, n_jobs=-1, cv=cvFold, scoring=“neg_mean_squared_error”) searchResults = gridSearch.fit(trainX, trainY) print(“[INFO] evaluating…”) bestModel = searchResults.best_estimator print(f”R2: bestModel.score(testX, testY)”) '''

Here is what each of the parameter in gridSearch will does:

• estimator: The model we’re attempting to optimize (i.e., our SVR that will predict the age of the abalone)
• param_grid: The hyperparameter search space
• n_jobs: The number of cores on your processor(s) that will be used to run parallel jobs. A value of -1 implies that all cores/processors will be used, thereby speeding the grid search process.
• scoring: The loss function we’re attempting to optimize; in this case, we are trying to drive down our mean squared error (MSE), implying that the lower the MSE, the better our model is at predicting the age of the abalone

After the grid search runs, we obtain the bestModel found during the search and then compute the determination coefficient, which will tell us how good of a job our model did.

Random search

In random search:

1. Define the hyperparameters we want to search over
2. Set a lower and upper bound on the values (if it’s a continuous variable) or the possible values the hyperparameter can take on (if it’s a categorical variable) for each hyperparameter
3. A random search then randomly samples from these distributions a total of N times, training a model on each set of hyperparameters
4. The hyperparameters associated with the highest accuracy model are then returned

While a random search, by definition, is not an exhaustive search like the grid search, the benefit of a random search is that it’s far faster and typically obtains just as high accuracy as a grid search. Lets now initialise our model and define the search pace of hyper parameters to perform the random-search over:

model = SVR()
kernel = ["linear", "rbf", "sigmoid", "poly"]
tolerance = loguniform(1e-6, 1e-3)
C = [1, 1.5, 2, 2.5, 3]
grid = dict(kernel=kernel, tol=tolerance, C=C)

Lets initialise cross-validation fold and perform a randomised-search to tune the hyperparameters:

print("[INFO] grid searching over the hyperparameters...")
cvFold = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
randomSearch = RandomizedSearchCV(estimator=model, n_jobs=-1,
	cv=cvFold, param_distributions=grid,
	scoring="neg_mean_squared_error")
searchResults = randomSearch.fit(trainX, trainY)
print("[INFO] evaluating...")
bestModel = searchResults.best_estimator_
print(f"R2: bestModel.score(testX, testY)")

Conclusion

Note that when tuning hyperparameters, there isn’t just one “golden set of values” that will give you the highest accuracy. Instead, it’s a distribution — there are rangesfor each hyperparameter that will obtain the best accuracy. If you land within that range/distribution, you’ll still enjoy the same high accuracy without the requirement of exhaustively tuning your hyperparameters with a grid search. This is why its suggested to use a randomised search instead of a grid search for hyper parameter tuning.